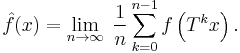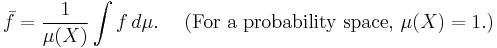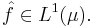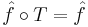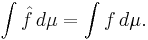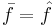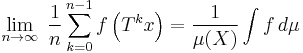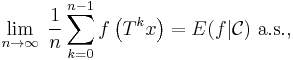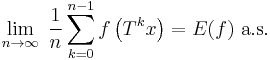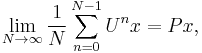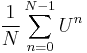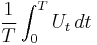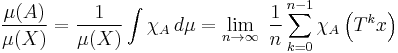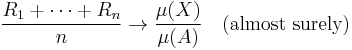Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics.
A central concern of ergodic theory is the behavior of a dynamical system when it is allowed to run for a long time. The first result in this direction is the Poincaré recurrence theorem, which claims that almost all points in any subset of the phase space eventually revisit the set. More precise information is provided by various ergodic theorems which assert that, under certain conditions, the time average of a function along the trajectories exists almost everywhere and is related to the space average. Two of the most important examples are ergodic theorems of Birkhoff and von Neumann. For the special class of ergodic systems, the time average is the same for almost all initial points: statistically speaking, the system that evolves for a long time "forgets" its initial state. Stronger properties, such as mixing and equidistribution, have also been extensively studied.
The problem of metric classification of systems is another important part of the abstract ergodic theory. An outstanding role in ergodic theory and its applications to stochastic processes is played by the various notions of entropy for dynamical systems.
The concepts of ergodicity and the ergodic hypothesis are central to applications of ergodic theory. The underlying idea is that for certain systems the time average of their properties is equal to the average over the entire space. Applications of ergodic theory to other parts of mathematics usually involve establishing ergodicity properties for systems of special kind. In geometry, methods of ergodic theory have been used to study the geodesic flow on Riemannian manifolds, starting with the results of Eberhard Hopf for Riemann surfaces of negative curvature. Markov chains form a common context for applications in probability theory. Ergodic theory has fruitful connections with harmonic analysis, Lie theory (representation theory, lattices in algebraic groups), and number theory (the theory of diophantine approximations, L-functions).
Ergodic transformations
Ergodic theory is often concerned with ergodic transformations.
Let T: X → X be a measure-preserving transformation on a measure space (X, Σ, μ), with 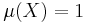 . A measure-preserving transformation T as above is ergodic if for every
. A measure-preserving transformation T as above is ergodic if for every
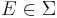 with
with 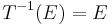 , then either
, then either 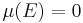 or
or 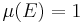 .
.
Examples
- An irrational rotation of the circle R/Z, T: x → x+θ, where θ is irrational, is ergodic. This transformation has even stronger properties of unique ergodicity, minimality, and equidistribution. By contrast, if θ = p/q is rational (in lowest terms) then T is periodic, with period q, and thus cannot be ergodic: for any interval I of length a, 0 < a < 1/q, its orbit under T (that is, the union of I, T(I), …, Tq-1(I), which contains the image of I under any number of applications of T) is a T-invariant mod 0 set that is a union of q intervals of length a, hence it has measure qa strictly between 0 and 1.
- Let G be a compact abelian group, μ the normalized Haar measure, and T a group automorphism of G. Let G* be the Pontryagin dual group, consisting of the continuous characters of G, and T* be the corresponding adjoint automorphism of G*. The automorphism T is ergodic if and only if the equality (T*)n(χ)=χ is possible only when n = 0 or χ is the trivial character of G. In particular, if G is the n-dimensional torus and the automorphism T is represented by an integral matrix A then T is ergodic if and only if no eigenvalue of A is a root of unity.
- A Bernoulli shift is ergodic. More generally, ergodicity of the shift transformation associated with a sequence of i.i.d. random variables and some more general stationary processes follows from Kolmogorov's zero-one law.
- Ergodicity of a continuous dynamical system means that its trajectories "spread around" the phase space. A system with a compact phase space which has a non-constant first integral cannot be ergodic. This applies, in particular, to Hamiltonian systems with a first integral I functionally independent from the Hamilton function H and a compact level set X = {(p,q): H(p,q)=E} of constant energy. Liouville's theorem implies the existence of a finite invariant measure on X, but the dynamics of the system is constrained to the level sets of I on X, hence the system possesses invariant sets of positive but less than full measure. A property of continuous dynamical systems that is the opposite of ergodicity is complete integrability.
Ergodic theorems
Let 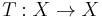 be a measure-preserving transformation on a measure space
be a measure-preserving transformation on a measure space 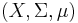 . One may then consider the "time average" of a
. One may then consider the "time average" of a  -integrable function f, i.e.
-integrable function f, i.e. 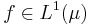 . The "time average" is defined as the average (if it exists) over iterations of T starting from some initial point x.
. The "time average" is defined as the average (if it exists) over iterations of T starting from some initial point x.
If 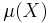 is finite and nonzero, we can consider the "space average" or "phase average" of f, defined as
is finite and nonzero, we can consider the "space average" or "phase average" of f, defined as
In general the time average and space average may be different. But if the transformation is ergodic, and the measure is invariant, then the time average is equal to the space average almost everywhere. This is the celebrated ergodic theorem, in an abstract form due to George David Birkhoff. (Actually, Birkhoff's paper considers not the abstract general case but only the case of dynamical systems arising from differential equations on a smooth manifold.) The equidistribution theorem is a special case of the ergodic theorem, dealing specifically with the distribution of probabilities on the unit interval.
More precisely, the pointwise or strong ergodic theorem states that the limit in the definition of the time average of f exists for almost every x and that the (almost everywhere defined) limit function 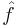 is integrable:
is integrable:
Furthermore, 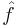 is T-invariant, that is to say
is T-invariant, that is to say
holds almost everywhere, and if 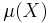 is finite, then the normalization is the same:
is finite, then the normalization is the same:
In particular, if T is ergodic, then 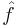 must be a constant (almost everywhere), and so one has that
must be a constant (almost everywhere), and so one has that
almost everywhere. Joining the first to the last claim and assuming that 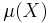 is finite and nonzero, one has that
is finite and nonzero, one has that
for almost all x, i.e., for all x except for a set of measure zero.
For an ergodic transformation, the time average equals the space average almost surely.
As an example, assume that the measure space 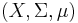 models the particles of a gas as above, and let f(x) denotes the velocity of the particle at position x. Then the pointwise ergodic theorems says that the average velocity of all particles at some given time is equal to the average velocity of one particle over time.
models the particles of a gas as above, and let f(x) denotes the velocity of the particle at position x. Then the pointwise ergodic theorems says that the average velocity of all particles at some given time is equal to the average velocity of one particle over time.
Probabilistic formulation: Birkhoff–Khinchin theorem
Birkhoff–Khinchin theorem. Let  be measurable,
be measurable, 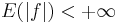 , and
, and  be a measure-preserving map. Then
be a measure-preserving map. Then
where 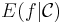 is the conditional expectation given the
is the conditional expectation given the  -algebra
-algebra  of invariant sets of
of invariant sets of  .
.
Corollary (Pointwise ergodic theorem) In particular, if  is also ergodic, then
is also ergodic, then  is the trivial
is the trivial  -algebra, and thus
-algebra, and thus
Mean ergodic theorem
Von Neumann's mean ergodic theorem, holds in Hilbert spaces.[1]
Let  be a unitary operator on a Hilbert space
be a unitary operator on a Hilbert space  ; more generally, an isometric linear operator (that is, a not necessarily surjective linear operator satisfying
; more generally, an isometric linear operator (that is, a not necessarily surjective linear operator satisfying 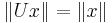 for all
for all 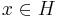 , or equivalently, satisfying
, or equivalently, satisfying 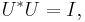 but not necessarily
but not necessarily 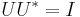 ). Let
). Let  be the orthogonal projection onto
be the orthogonal projection onto 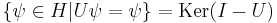 .
.
Then, for any 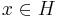 , we have:
, we have:
where the limit is with respect to the norm on H. In other words, the sequence of averages
converges to P in the strong operator topology.
This theorem specializes to the case in which the Hilbert space H consists of L2 functions on a measure space and U is an operator of the form
where T is a measure-preserving endomorphism of X, thought of in applications as representing a time-step of a discrete dynamical system.[2] The ergodic theorem then asserts that the average behavior of a function f over sufficiently large time-scales is approximated by the orthogonal component of f which is time-invariant.
In another form of the mean ergodic theorem, let Ut be a strongly continuous one-parameter group of unitary operators on H. Then the operator
converges in the strong operator topology as T → ∞. In fact, this result also extends to the case of strongly continuous one-parameter semigroup of contractive operators on a reflexive space.
Remark: Some intuition for the mean ergodic theorem can be developed by considering the case where complex numbers of unit length are regarded as unitary transformations on the complex plane (by left multiplication). If we pick a single complex number of unit length (which we think of as  ), it is intuitive that its powers will fill up the circle. Since the circle is symmetric around 0, it makes sense that the averages of the powers of
), it is intuitive that its powers will fill up the circle. Since the circle is symmetric around 0, it makes sense that the averages of the powers of  will converge to 0. Also, 0 is the only fixed point of
will converge to 0. Also, 0 is the only fixed point of  , and so the projection onto the space of fixed points must be the zero operator (which agrees with the limit just described).
, and so the projection onto the space of fixed points must be the zero operator (which agrees with the limit just described).
Convergence of the ergodic means in the Lp norms
Let 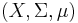 be as above a probability space with a measure preserving transformation T, and let
be as above a probability space with a measure preserving transformation T, and let 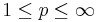 . The conditional expectation with respect to the sub-σ-algebra
. The conditional expectation with respect to the sub-σ-algebra 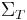 of the T-invariant sets is a linear projector
of the T-invariant sets is a linear projector 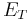 of norm 1 of the Banach space
of norm 1 of the Banach space 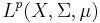 onto its closed subspace
onto its closed subspace 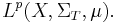 The latter may also be characterized as the space of all T-invariant
The latter may also be characterized as the space of all T-invariant 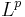 -functions on X. The ergodic means, as linear operators on
-functions on X. The ergodic means, as linear operators on 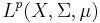 also have unit operator norm; and, as a simple consequence of the Birkhoff–Khinchin theorem, converge to the projector
also have unit operator norm; and, as a simple consequence of the Birkhoff–Khinchin theorem, converge to the projector 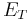 in the strong operator topology of
in the strong operator topology of 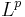 if
if 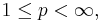 and in the weak operator topology if
and in the weak operator topology if 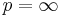 . More is true if
. More is true if 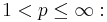 then the Wiener–Yoshida–Kakutani ergodic dominated convergence theorem states that the ergodic means of
then the Wiener–Yoshida–Kakutani ergodic dominated convergence theorem states that the ergodic means of 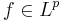 are dominated in
are dominated in 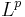 ; however, if
; however, if 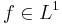 , the ergodic means may fail to be equidominated in
, the ergodic means may fail to be equidominated in 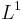 . Finally, if f is assumed to be in the Zygmund class, that is
. Finally, if f is assumed to be in the Zygmund class, that is 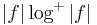 is integrable, then the ergodic means are even dominated in
is integrable, then the ergodic means are even dominated in 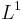 .
.
Sojourn time
Let 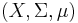 be a measure space such that
be a measure space such that 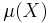 is finite and nonzero. The time spent in a measurable set A is called the sojourn time. An immediate consequence of the ergodic theorem is that, in an ergodic system, the relative measure of A is equal to the mean sojourn time:
is finite and nonzero. The time spent in a measurable set A is called the sojourn time. An immediate consequence of the ergodic theorem is that, in an ergodic system, the relative measure of A is equal to the mean sojourn time:
for all x except for a set of measure zero, where 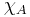 is the indicator function of A.
is the indicator function of A.
Let the occurrence times of a measurable set A be defined as the set k1, k2, k3, ..., of times k such that Tk(x) is in A, sorted in increasing order. The differences between consecutive occurrence times Ri = ki − ki−1 are called the recurrence times of A. Another consequence of the ergodic theorem is that the average recurrence time of A is inversely proportional to the measure of A, assuming that the initial point x is in A, so that k0 = 0.
(See almost surely.) That is, the smaller A is, the longer it takes to return to it.
Ergodic flows on manifolds
The ergodicity of the geodesic flow on compact Riemann surfaces of variable negative curvature and on compact manifolds of constant negative curvature of any dimension was proved by Eberhard Hopf in 1939, although special cases had been studied earlier: see for example, Hadamard's billiards (1898) and Artin billiard (1924). The relation between geodesic flows on Riemann surfaces and one-parameter subgroups on SL(2,R) was described in 1952 by S. V. Fomin and I. M. Gelfand. The article on Anosov flows provides an example of ergodic flows on SL(2,R) and on Riemann surfaces of negative curvature. Much of the development described there generalizes to hyperbolic manifolds, since they can be viewed as quotients of the hyperbolic space by the action of a lattice in the semisimple Lie group SO(n,1). Ergodicity of the geodesic flow on Riemannian symmetric spaces was demonstrated by F. I. Mautner in 1957. In 1967 D. V. Anosov and Ya. G. Sinai proved ergodicity of the geodesic flow on compact manifolds of variable negative sectional curvature. A simple criterion for the ergodicity of a homogeneous flow on a homogeneous space of a semisimple Lie group was given by Calvin C. Moore in 1966. Many of the theorems and results from this area of study are typical of rigidity theory.
In the 1930s G. A. Hedlund proved that the horocycle flow on a compact hyperbolic surface is minimal and ergodic. Unique ergodicity of the flow was established by Hillel Furstenberg in 1972. Ratner's theorems provide a major generalization of ergodicity for unipotent flows on the homogeneous spaces of the form Γ\G, where G is a Lie group and Γ is a lattice in G.
In the last 20 years, there have been many works trying to find a measure-classification theorem similar to Ratner's theorems but for diagonalizable actions, motivated by conjectures of Furstenberg and Margulis. An important partial result (solving those conjectures with an extra assumption of positive entropy) was proved by Elon Lindenstrauss, and he was awarded the Fields medal in 2010 for this result.
See also
- Chaos theory
- Ergodic hypothesis
- Ergodic process
- Maximal ergodic theorem
- Statistical mechanics
- Symbolic dynamics
References
- ^ I: Functional Analysis : Volume 1 by Michael Reed, Barry Simon,Academic Press; REV edition (1980)
- ^ (Walters 1982)
Historical references
- Birkhoff, George David (1931), "Proof of the ergodic theorem", Proc Natl Acad Sci USA 17 (12): 656–660, Bibcode 1931PNAS...17..656B, doi:10.1073/pnas.17.12.656, PMC 1076138, PMID 16577406, http://www.pnas.org/cgi/reprint/17/12/656.
- Birkhoff, George David (1942), "What is the ergodic theorem?", American Mathematical Monthly (The American Mathematical Monthly, Vol. 49, No. 4) 49 (4): 222–226, doi:10.2307/2303229, JSTOR 2303229.
- von Neumann, John (1932), "Proof of the Quasi-ergodic Hypothesis", Proc Natl Acad Sci USA 18 (1): 70–82, Bibcode 1932PNAS...18...70N, doi:10.1073/pnas.18.1.70, PMC 1076162, PMID 16577432, http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1076162.
- von Neumann, John (1932), "Physical Applications of the Ergodic Hypothesis", Proc Natl Acad Sci USA 18 (3): 263–266, Bibcode 1932PNAS...18..263N, doi:10.1073/pnas.18.3.263, JSTOR 86260, PMC 1076204, PMID 16587674, http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1076204.
- Hopf, Eberhard (1939), "Statistik der geodätischen Linien in Mannigfaltigkeiten negativer Krümmung", Leipzig Ber. Verhandl. Sächs. Akad. Wiss. 91: 261–304.
- Fomin, Sergei V.; Gelfand, I. M. (1952), "Geodesic flows on manifolds of constant negative curvature", Uspehi Mat. Nauk 7 (1): 118–137.
- Mautner, F. I. (1957), "Geodesic flows on symmetric Riemann spaces", Ann. Math. (The Annals of Mathematics, Vol. 65, No. 3) 65 (3): 416–431, doi:10.2307/1970054, JSTOR 1970054.
- Moore, C. C. (1966), "Ergodicity of flows on homogeneous spaces", Amer. J. Math. (American Journal of Mathematics, Vol. 88, No. 1) 88 (1): 154–178, doi:10.2307/2373052, JSTOR 2373052.
Modern references
- D.V. Anosov (2001), "Ergodic theory", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=e/e036150
- This article incorporates material from ergodic theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
- Vladimir Igorevich Arnol'd and André Avez, Ergodic Problems of Classical Mechanics. New York: W.A. Benjamin. 1968.
- Leo Breiman, Probability. Original edition published by Addison–Wesley, 1968; reprinted by Society for Industrial and Applied Mathematics, 1992. ISBN 0-89871-296-3. (See Chapter 6.)
- Peter Walters, An introduction to ergodic theory, Springer, New York, 1982, ISBN 0-387-95152-0.
- Tim Bedford, Michael Keane and Caroline Series, eds. (1991), Ergodic theory, symbolic dynamics and hyperbolic spaces, Oxford University Press, ISBN 0-19-853390-X (A survey of topics in ergodic theory; with exercises.)
- Karl Petersen. Ergodic Theory (Cambridge Studies in Advanced Mathematics). Cambridge: Cambridge University Press. 1990.
- Joseph M. Rosenblatt and Máté Weirdl, Pointwise ergodic theorems via harmonic analysis, (1993) appearing in Ergodic Theory and its Connections with Harmonic Analysis, Proceedings of the 1993 Alexandria Conference, (1995) Karl E. Petersen and Ibrahim A. Salama, eds., Cambridge University Press, Cambridge, ISBN 0-521-45999-0. (An extensive survey of the ergodic properties of generalizations of the equidistribution theorem of shift maps on the unit interval. Focuses on methods developed by Bourgain.)
- A.N. Shiryaev, Probability, 2nd ed., Springer 1996, Sec. V.3. ISBN 0-387-94549-0.
External links
- Ergodic Theory (29 October 2007) Notes by Cosma Rohilla Shalizi
- Ergodic theorem passes the test From Physics World